катЯRтак
(R)
- Глава 15
СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Что еще можно обнаружить в преобразованиях Лоренца? Любопытно, что в них преобразование x и t по форме похоже на преобразование x и t, изученное в гл. 11, когда мы говорили о вращении координат. Тогда мы получили
т. е. новое x' перемещает старые x и y, а y' тоже их перемешивает. Подобным же образом в преобразовании Лоренца новое x' есть смесь старых x и t, а новое t' - смесь t и x. Значит, преобразование Лоренца похоже на вращение, но "вращение" в пространстве и времени. Это весьма странное понятие. Проверить аналогию с вращением можно, вычислив величину
В этом уравнении три первых члена в каждой строне представляют собой в трехмерной геометрии квадрат расстояния между точкой и началом координат (сферу). Он не меняется (остается инвариантным), несмотря на вращение осей координат. Аналогично, уравнение (
15.9) свидетельствует о том, что существует определенная комбиниция координат и времени, которая остается инвариантной при преобразовании Лоренца. Значит, имеется полная аналогия с вращением; аналогия эта такого рода, что векторы, т. е. величины, составленные из "компонент", преобразуемых так же, как и координаты, оказываются полезными и в теории относительности.
Итак, мы расширим понятие вектора. Пока он у нас мог иметь только пространственные компоненты. Теперь включим в это понятие и временную компоненту, т. е. мы ожидаем, что существуют векторы с четырьмя компонентами: три из них похожи на компоненты обычного вектора, а к ним привязана четвертая - аналог времени.
В следующих главах мы проанализируем это понятие. Мы увидим, что если идеи этого параграфа приложить к импульсу, то преобразование даст три пространственные составляющие, подобные обычным компонентам импульса, и четвертую компоненту - временную часть (которая есть не что иное, как энергия).
Теперь мы готовы к тому, чтобы с более общей точки зрения исследовать, как преобразования Лоренца изменяют законы механики. [До сих пор мы только обЪясняли, как изменяются длины и времена, но не объяснили, как получить измененную формулу для
m, уравнение (
15.1). Это будет сделано в следующей главе.] Изучение следствий формулы Эйнштейна для массы
m в механике Ньютона мы начнем с закона силы. Сила есть быстрота изменения импульса, т. е.
Импульс по-прежнему равен mv, но теперь
Это законы Ньютона в записи Эйнштейна. При этом видоизменении, если действие и противодействие по-прежнему равны (может, не в каждый момент, но по крайней мере после усреднения времени), то, как и раньше, импульс должен сохранятся, но сохраняющейся величиной является не старое
mv при постоянном
m, а выражение (
15.10) с переменной массой. С таким названием в формуле для импульса сохранение импульса по-прежнему будет существовать.
Посмотрим теперь, как импульс зависит от скорости. В ньютоновой механике он ей прпорционален. В релятивистской механике в большом интервале скоростей (много меньших
c) они также примерно пропорциональны [см. (
15.10)], потому что корень мало отличается от единицы. Но когда
v почти равно
c, то корень почти равен нулю и импульс поэтому беспредельно растет.
Что бывает, когда на тело долгое время воздействует постоянная сила? В механике Ньютона скорость тела беспрерывно будет возрастать и может превысить даже скорость света. В релятивистской же механике это невозможно. В теории относительности беспрерывно растет не скорость тела, а его импульс, и рост этот сказывается не на скорости, а на массе тела. Со временем ускорение, т. е. изменения в скорости, практически исчезает, но импульс продолжает расти. Поскольку сила приводит к очень малым изменениям в скорости тела, мы, естественно, считаем, что у тела громадная инерция. Но как раз это самое и утверждает релятивистская формула (15.10) для массы тела; она говорит, что инерция крайне велика, когда
v почти равно
c. Разберем пример. Чтобы отклонить быстрые электроны в синхротроне Калифорнийского Технологического института, необходимо магнитное поле, в 2000 раз более сильно, чем следует из законов Ньютона. Иными словами, масса электронов в синхротроне в 2000 раз больше их нормальной массы, достигая массы протона! Если
m в 2000 раз больше
m0 , то 1-
m2/
c2 равно 1/4 000 000, или
v отличается от
c на 1/8 000 000, т. е. скорость электронов вплотную подходит к скорости света. Если электроны и свет одновременно отправятся в соседнюю лабораторию (находящуюся, скажем, в 200 м), то кто явится первым? Ясное дело свет: он всегда движется
быстрее*. Но насколько быстрее? Трудно сказать, насколько раньше во времени, но зато можно сказать, на какое расстояние отстанут электроны: на
1/
30мм, т. е. на
1/
3 толщины этого листка бумаги! Масса электронов в этих состязаниях чудовищна, а скорость не выше скорости света.
На чем еще скажется релятивистский рост масы? Рассмотрим движение молекул газа в балоне. Если газ нагреть, скорость молекул возрастает, а вместе с нею и их масса. Газ станет тяжелее. Насколько?
Разлагая
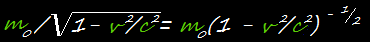
в ряд по формуле бинома Ньютона, можно найти приближенно рост массы при малых скоростях. Получается
Из формулы ясно, что при малых v ряд быстро сходится и первых двух-трех членов здесь вполне достаточно. Значить, можно написать
где второй член и выражает рост массы за счет повышения скорости. Когда растет температура,
v2 растет в равной мере, значит, увеличение массы пропорционально повышению температуры. Но
1/
2m0v2 - это кинетическая энергия в староводном, ньютоновском смысле этого слова. Значит, можно сказать, что прирост массы газа равен приросту кинетической энергии, деленной на
c2, т. е.

*Правда,
видимый свет проиграет гонку из-за преломления в воздухе. А
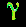
- излучение ее, несомненно, выиграет.
Это наблюдение навело Эйнштейна на мысль, что массу тела можно выразить проще, чем по формуле (15.1), если сказать, что масса равна полному содержанию энергии в теле, деленному на c2. Если (15.11) помножить на c2, получается
Здесь левая часть дает полную энергию тела, а в последнем члене справа мы узнаем обычную кинетическую энергию. Эйнштейн осмыслил первый член справа (очень большое постоянное число m0c2) как часть полной энергии тела, а именно как его внутреннюю энергию, или "энергию покоя".
К каким следствиям мы придем, если вслед за Эйнщтейном предположим, что "энергия тела всегда равна"
mc2? Тогда мы сможем вывести формулу (
15.1) зависимости массы от скорости, ту самую, которую до сих пор мы принимали на веру. Пусть тело сперва покоится, обладая энергией
m0c2) Затем мы прикладываем к телу силу которая сдвигает его с места и поставляет ему кинетическую энергию; раз энергия примется возрастать, то начинает расти и масса (это все заложено в первоначальном предположении). Пока сила действует, энергия и масса продолжают расти. Мы уже видели (см.
гл. 13), что быстрота роста энергии со временем равна произведению силы на скорость
***
В обычных условиях изменения энергии приводят к очень малым изменениям в массе: почти никогда не удается из данного количества вещества извлечь много энергии; но в атомной бомбе с энергией взрыва, эквивалентной 20 000 тонн тринитротолуола, весь пепел, осевший после взрыва, на 1 г легче первоначального количества расщепляющего материала. Это потому, что выделилась энергия, которая имела массу 1 г, в согласии с формулой

. Вывод об эквивалентности массы и энергии прекрасно подтвердился в опытах по аннигиляции материи - превращению вещества в энергию. Электрон с позитроном могут взаимодействовать в покое, имея каждый массу покоя
m0. При сближении они исчезают, а вместо них излучаются два
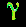
- луча, каждый опять с энергией
m0c2. Этот опыт прямо сообщает нам о величине энергии, связанной с существованием массы покоя у частицы.


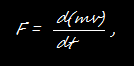
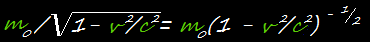 в ряд по формуле бинома Ньютона, можно найти приближенно рост массы при малых скоростях. Получается
в ряд по формуле бинома Ньютона, можно найти приближенно рост массы при малых скоростях. Получается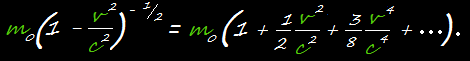

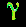 - излучение ее, несомненно, выиграет.
- излучение ее, несомненно, выиграет. . Вывод об эквивалентности массы и энергии прекрасно подтвердился в опытах по аннигиляции материи - превращению вещества в энергию. Электрон с позитроном могут взаимодействовать в покое, имея каждый массу покоя m0. При сближении они исчезают, а вместо них излучаются два
. Вывод об эквивалентности массы и энергии прекрасно подтвердился в опытах по аннигиляции материи - превращению вещества в энергию. Электрон с позитроном могут взаимодействовать в покое, имея каждый массу покоя m0. При сближении они исчезают, а вместо них излучаются два 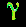 - луча, каждый опять с энергией m0c2. Этот опыт прямо сообщает нам о величине энергии, связанной с существованием массы покоя у частицы.
- луча, каждый опять с энергией m0c2. Этот опыт прямо сообщает нам о величине энергии, связанной с существованием массы покоя у частицы.