(ct3)2 = L2 + (ut3)2
- Глава 15
СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Свыше двухсот лет считалось, что уравнения движения, провозглашенные Ньютоном, правильно описывали природу. Потом в них была обнаружена ошибка. Обнаружена и тут же исправлена. И заметил ошибку, и исправил ее в 1905 г. один и тот же человек - Эйнштейн.
Второй закон Ньютона, выражаемый уравнением
безмолвно предполагал, что m - величина постоянная. Но теперь мы знаем, что это не так, что масса тела возрастает со скоростью. В формуле, исправленной Эйнштейном, m появилась в таком виде:
Здесь "масса покоя" m0 - это масса неподвижного тела, а c - скорость света (примерно 3x105 км/сек).
Для кого теория нужна лишь для решения задач, тому этой формулы будет вполне достаточно. Больше ничего от теории относительности ему не понадобится; он просто введет в законы Ньютона поправку на изменяемость массы. Из самой формулы очевидно, что рост массы в обычных условиях незначителен.
Даже если v - скорость спутника (около 8км/сек), то и при этих условиях v/c = 3/105; подстановка этой величины в формулу показывает, что поправка к массе составит не более одной двухмиллиардной части самой массы, что, пожалуй, заметить невозможно. На самом деле, правильность формулы подтверждена наблюдением движения разнообразных частиц, скорость которых практически вплотную подходила к скорости света. В обычных условиях рост массы незаметен; тем замечательней, что он сперва был обнаружен теоретически, а уж после открыт на опыте. Хотя для достаточно больших скоростей рост может быть как угодно велик, открыт он был не таким путем. Закон этот в момент своего открытия означал лишь едва заметное изменение в цифрах. Тем интереснее разобраться, как сочетание физического размышления и физического эксперимента вызвало его к жизни. Вклад в это дело внесло немалое число людей, но конечным итогом их деятельности явилось открытие Эйнштейна.
У Эйнштейна, собственно говоря, есть две теории относительности. Мы будем здесь гворить только о специальной теории относительности, ведущей свое начало с 1905 г. В 1915 г. Эйнштейн выдвинул еще одну теорию, называемую общей теорией относительности. Она обобщает специальную теорию на случай тяготения; мы не будем ее здесь обсуждать.
Принцип относительности впервые высказал Ньютон в одном из следствий законов движения: "Относительные движения друг по отношению к другу тел, заключенных в каком-либо пространстве, одинаковы, покоится ли это пространство или движется равномерно и прямолинейно без вращения". Это означает, к примеру, что при полете межпланетного корабля с постоянной скоростью все опыты, поставленные на этом корабле, все явления, наблюдаемые на нем, будут таковы, как будто он покоится (конечно, при условии, что наружу из корабля выходить не будут). В этом смысл принципа относительности. Мысль эта - довольно проста; вопрос толко в том, верно ли, что во всех опытах, производимых внутри движущейся системы, законы физики выглядят такими же, какими они были бы, если бы система стояла на одном месте. Давайте же сначала посмотрим, так ли выглядят законы Ньютона в движущейся системе. Для этого нам снова понадобится помощь наших молодых людей - Мика и Джо.
Пуска Мик отправился по оси x с постоянной скоростью u и измеряет свое положение в какой-то точке, показанной на фиг. 15.1. Он обозначает "x - расстояние" точки в своей системе координат как x'. Джо стоит на месте и измеряет положение той же точки, обозначая ее x-координату в своей системе через x. Связ между координатами в двух системах ясна из рисунка. За время t начало системы Мика сдвинулось на ut, и если обе системы в начале совпадали, то
Если подставить эти преобразования координат в законы Ньютона, то законы эти превращаятся в такие же законы, но в штрихованной системе; это значить, что законы Ньютона имеют одинаковый вид в движущейся и неподвижной системах; поэтому-то, проделав любые опыты по механике, и нельзя сказать, движется система или нет.
Принцип относительности применялся в механике уже издавна. Многие, в частности Гюйгенс, пользовались им для вывода законов столкновения биллиардных шаров почти так же, как мы в гл. 10* доказывали сохранение импульса.
В прошлом столетии в результате исследований явлений электричества, магнетизма и света интерес к принципу относительности возрос. Максвелл подытожил в своих уравнениях электромагнитного поля многие тщательные исследования этих явлений. Его уравнения сводят воедино электричество, магнетизм, свет. Однако уравнения Максвелла, по-видимому не подчиняются принципу относительности: если преобразовать их подстановкой (15.2), то их вид не останется прежним. Значит в движущемся межпланетном корабле оптические и электрические явления не такие, как в неподвижном; их можно использовать для определения его скорости, в частности определить и абсолютную скорость корабля, сделав подходящие электрические и оптические измерения. Одно из следствий уравнения Максвела заключается в том, что если возмущение поля порождает свет, то эти электромагнитные волны распространяются во все стороны одинаково и с одинаковой скоростью c = 300 000 км/сек. Другое следствие уравнений: если источник возмущения движется, то испускаемый свет все равно движется сквозь пространство со скоростью c. Так же бывает и со звуком: скорость звуковых волн тоже не зависит от движения источника.
Эта независимость от источника света ставит интересный вопрос. Положим, что мы едем в автомашине со скоростью u, а свет фар распространяется со скоростью c. Дифференцируя первую строчку в (15.2), получаем
Это означает, что, в согласии с преобразованиями Галилея, видимая скорость света по измерениям, проведенным из автомашины, будет не c, а c - u. Наример, скорость автомашины 100 000 км/сек, а скорость света 300 000 км/сек, тогда свет от фар будет удалятся с быстротой 200 000 км/сек. Во всяком случае, измерив скорость света, испускаемого фарами (если только справедливы преобразования Галилея для света фар), можно узнать скорость автомашины. На этой идее основывалось множество опытов по определению скорости Земли, но ни один из них не удался: никакой скорости обнаружено не было. Вы скоро познакомитесь очень подробно с одним из таких опытов. Вы разберетесь, что в нем случилось и в чем было дело. Что-то неладное творилось в ту пору с уравнениями физики. Но что именно?
Когда стало ясно, что с уравнениями физики не все ладится, первым долгом подозрение пало на уравнения электродинамики Максвелла. Они только-только были написаны, им было всего 20 лет от роду; казалось почти естественным, что они неверны. Их принялись переписывать, видоизменять и подгонять к тому, чтобы оказался выполненным принцип относительности в галилеевой форме (
15.2). При этом в уравнениях электродинамики появились новые члены; они предсказывали новые электрические явления, но эксперимент никаких таких явлений не обнаружил, и пришлось отказаться изменить уравнения Максвелла. Постепенно всем становилось ясно, максвелловы законы электродинамики абсолютно правильны, а загвоздка в чем-то другом.
Между тем Лоренц замети одно замечательно любопытное явление: когда он делал в уравнениях Максвелла подстановку

То форма уравнений после подстановки не менялась! Уравнения (15.3) теперь называют преобразованиями Лоренца. А Эйнштейн, следуя мысли, впервые высказаной Пуанкаре, предположил, что
все физические законы не должны меняться от преобразований Лоренца. Иными словами, надо менять не законы электродинамики, а законы механики. Но как же изменить законы Ньютона, чтобы
они при преобразованиях Лоренца не менялись? Когда такая цель поставлена, то остается только переписать уравнения Ньютона так, чтобы выполнялись поставленные условия. Как оказалось, единственное, что нужно от них потребовать, - зто, чтоб масса
m в уравнениях Ньютона приобрела вид (
15.1). Стоит внести это изменение, и наступает полная гармония между уравнениями Ньютона и Максвелла. Если вы теперь, желая согласовать измерения, проведенные Миком и Джо, используете преобразования Лоренца, то вы ни за что не узнаете, кто из них движется, ибо форма всех уравнений в обеих системах координат будет одной и той же!
Интересно понять, что означает эта замена старых преобразований координат и времени на новые. Старые (галилеевы) кажутся очевидными, новые (лоренцевы) выглядят необычно. Как же это может быть, с логической и экспериментальной точек зрения, что справедливы не старые преобразования, а новые? Чтобы разобраться в этом, мало изучить законы механики, надо (как это и сделал Эйнштейн) проанализировать и наши представления о прстранстве и времени, иначе этих преобразований не поймешь. В течении некоторого времени мы мы будем изучать эти представления и следствия из них. Покамест же стоит отметить, что такой анализ оказывается вполне оправданным - его результаты согласуются с данными опыта.
Мы уже говорили, что в свое время были сделаны попытки определить абсолютную скорость движения Земли сквозь воображаемый "эфир", который, как думали тогда, пропитывает собой все пространство. Самый известный из таких опытов проделали в 1887 г. Майкельсон и Морли. Но только через 18 лет отрицатеьные результаты их опыта объяснил Эйнштейн.
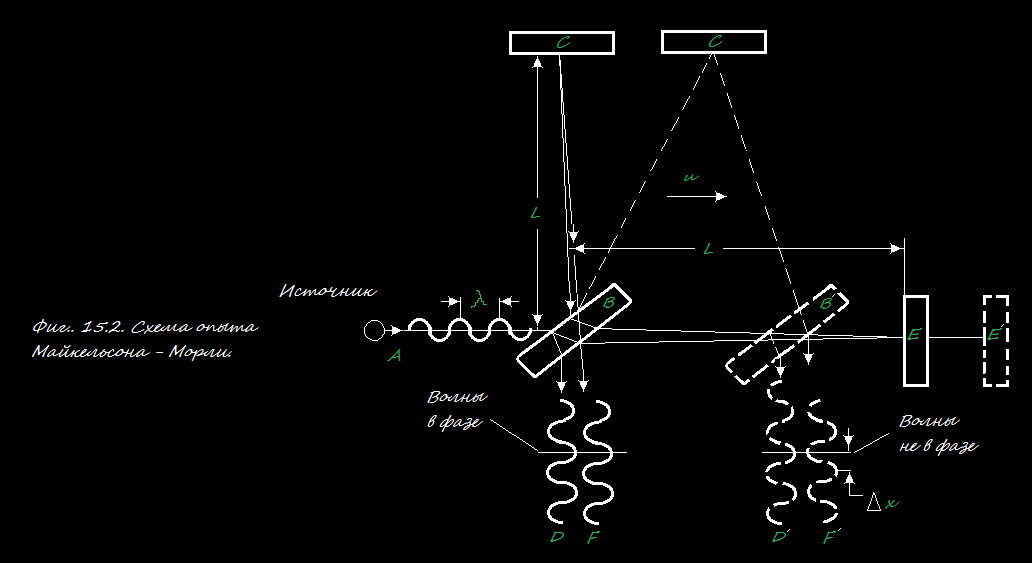
Для опыта Майкельсона - Морли использовался прибор, схема которого показана на фиг. 15.2 Главные части прибора: источник света A, посеребренная полупрозрачная стеклянная пластинка B, два зеркала C и E. Все это жестко укрепляется на тяжелой плите. Зеркала C и E размещены были на одинаковом расстоянии L от пластинки B. Пластинка B расщепляет падающий пучок света на два, перпендикулярных один к другому; они направляются на зеркала и отражаются обратно на пластинку B. Пройдя сквозь пластинку B, оба пучка накладываются друг на друга (D и F). Если время прохождения света от B до E и обратно равно времени прохождения от B до C и обратно, то возникающие пучки D и F окажутся в фазе и усилятся взаимно; если же эти времена хоть немного отличаются, то в пучках возникает сдвиг по фазе и, как следствие, - интерференция. Если прибор в эфире "покоится", то времена в точности равны, а если он движется направо со скоростью u, то появится разница во времени. Давайте посмотрим почему.
Сначала подсчитаем время прохождения света от B к E и обратно. Пусть время "туда" равно t1, а время "обратно" равно t2. Но пока свет движется от B до зеркала, сам прибор уйдет на расстояние ut1, так что свету прийдется пройти путь L+ut1 со скоростью c. Этот путь можно поэтому обозначить и как ct1; следовательно,
ct1 = L + ut1, или t1 = L/(c - u)
(этот результат становится очевидным, если учесть, что скорость света по отношению к прибору есть c-u). Точно так же можно расчитать и t2. За это время пластинка B приблизится на расстояние ut2, так что свету на обратном пути придется пройти только L-ut2. Тогда
ct2 = L - ut2, или t2 = L/(c + u)
Общее же время равно
t1+t2 = 2Lc/(c2- u2);
Удобнее зто записаиь в виде
А теперь подсчитаем, сколько времени t3 свет будет идти от пластинки B до зеркала C. Как и прежде, за время t3 зеркало C сдвинется направо на расстояние ut3 до положения C'), а свет пройдет по гипотенузе BC' расстояние ct3. Из
прямоугольного треугольника следует
(ct3)2 = L2 + (ut3)2
или
L2 = c2t32 - u2t32 = (c2-u2)t32,
откуда
При обратной прогулке от точки C ' свету приходится пройти то же расстояние; это видно из симметрии рисунка. Значит, и время прохождения то же (t3), а общее время равно 2t3. Мы запишем его в виде
Теперь мы можем сравнить оба времени. Числители в (
15.4) и (
15.5) одинаковы - это время распространения света в покоящемся приборе. В знаменалях член
u2/
c2 мал, если только
u много меньше
c. Знаменатели эти показывают, насколько изменяется время из-за движения прибора. Заметьте, что эти изменения
неодинаковы - время прохождения света до
C и обратно чуть меньше времени прохождения до
E и обратно. Они не совпадают, даже если расстояния зеркал до
B одинаковы. Остается только точно измерить эту разницу.
Здесь возникает одна техническая тонкость: а что если длины L не точно равны между собой? Ведь точного равенства все равно никогда не добьешься. В этом случае надо просто повернуть прибор на 90o, а расположив BC по движению, а BE - поперек. Различие в длинах тогда перестает играть роль, и остается только наблюдать за сдвигом интерференционных полос при повороте прибора.
Во время опыта Майкельсон и Морли расположили прибор так, что отрезок BE оказался параллельным движению Земли по орбите (в определенный час дня и ночи). Орбитальная скорость равна примерно 30 км/сек, и "снос эфира" в определенные часы дня или ночи и в определенное время года должен достигать этой величины. Прибор был достаточно чувствителен, чтобы заметить такое явление. Но никакого различия во временах обнаружено не было - скорость движения Земли сквозь эфир оказалось невозможно обнаружить. Результат опыта был нулевой.
Это было загадочно. Это настораживало. Первую плодотворную идею, как выйти из тупика, выдвинул Лоренц. Он допустил, что все материальные тела при движении сжимаются, но только в направлении движения. Таким образом, если длина покоящегося тела есть L0 , то длина тела, движущегося со скоростью u (назовем ее L|| , где значок || показывает, что движение происходит вдоль длинны тела), дается формулой
Если эту формулу применить к интерферометру Майкельсона - Морли, то расстояние от
B до
C остается прежним, а расстояние от
B до
C остается прежним, а расстояние от
B до
E укоротится до

. Таким образом, уравнение (
15.5) не изменится, но
L в уравнении (
15.4) изменится в соответствии с (
15.6) в результате мы получим
Сравнивая это с (
15.5), мы видим, что теперь
t1 +
t2 = 2
t3. Стало быть, если прибор действительно сокращяется так, как мы предположили, то становится понятным, почему опыт Майкельсона - Морли никакого эффекта не дал.
Хотя гипотеза гипотеза сокращения успешно объясняла отрицательный итог опыта, она сама оказалась беззащитной перед обвинением, что ее единственная цель - избавиться от трудностей в объяснении опыта. Она была чересчур искуственной. Однако сходные трудности возникали и в других опытах по обнаружению эфирного ветра. В конце концов стало казаться, что природа вступила в "заговор" против человека, что она прибегла к конспирации и то и дело вводит какие-то новые явления, чтобы свести к нулю каждое явление, с помощью которого человек пытается измерить u.
И наконец, было признано (на это указал Пуанкаре), что полная конспирация - это и есть закон природы! Пуанкаре предположил, что в природе есть закон, заключающийся в том, что нельзя обнаружить эфирный ветер никаким способом, т. е. абсолютную скорость обнаружить невозможно.
***
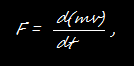
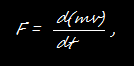
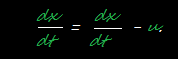

 . Таким образом, уравнение (15.5) не изменится, но L в уравнении (15.4) изменится в соответствии с (15.6) в результате мы получим
. Таким образом, уравнение (15.5) не изменится, но L в уравнении (15.4) изменится в соответствии с (15.6) в результате мы получим