(R)
ДРУГИЕ СИСТЕМЫ С ДВУМЯ СОСТОЯНИЯМИ
§ 2. Ядерные силы.
§ 3. Молекула водорода
§ 4. Молекула бензола
§ 5. Красители
§ 6. Гамильтониан частицы со спином х/2 в магнитном поле
§ 7. Вращающийся электрон в магнитном поле
В предыдущей главе мы обсудили некотоpые свойства молекулы аммиака в предположении, что это система о двух состояниях (или двухуровневая система). На самом деле, конечно, это не так — у нее есть множество состояний: вращения, колебания, перемещения т, д., но в каждом из этих состояний движения следует говорить о паре внутренних состояний из-за того, что атом азота может быть переброшен с одной стороны плоскости трех атомов водорода на другую. Сейчас мы рассмотрим другие примеры систем, которые в том или ином приближении можно будет считать системами с двумя состояниями. Многое здесь будет приближенным, потому что всегда имеется множество других состояний, и в более точном анализе их следовало бы учитывать. Но в каждом из этих примеров мы окажемся в силах очень многое понять, рассуждая только о двух состояниях.
Раз мы будем иметь дело только с двухуровневыми системами, то нужный нам гамильтониан будет выглядеть так же, как и в предущей главе. Когда гамильтониан не зависит от времени, то известно, что имеются два стационарных состояния с определенными (и обычно разными) энергиями. В общем случае однако, мы будем начинать наш анализ с выбора базисных состояний (не обязательно этих стационарных состояний), таких, которые, скажем имеют другой простой физический смысл. Тогда стационарные состояния системы будут представлены линейной комбинацией этих базисных состояний.
Для удобства подытожим важнейшие уравнения, выведенные в гл. 7. Пусть первоначально в качестве базисных состояний были приняты |1> и |2>. Тогда любое состояние

представляется их линейной комбинацией:
 (8.1)
(8.1)Амплитуды Ci (под этим подразумеваются как C1 так и C2 ) удовлетворяют двум линейным дифференциальным уравнениям
 (8.2)
(8.2)где и i, и j принимают значения 1 и 2.
Когда члены гамильтониана Hi j не зависят от t, то два состояния с определенной энергией (стационарные), которые мы обозначим
обладают энергиями
Для каждого из этих состояний оба C имеют одинаковую зависимость от времени. Векторы состояний |I> и |II>, которые отвечают стационарным состояниям, связаны с нашими первоначальными базисными состояниями |1> и |2> формулами
Здесь a — комплексные постоянные, удовлетворяющие равенствам
Если H11 и H22 между собой равны, скажем оба равны E0 , а H12 = H21 = —A, то EI + E0 + A, EII + E0 - A, и состояния |I> и |II> особенно просты:
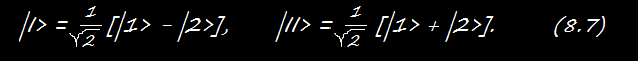

Эти результаты мы хотим теперь использовать, чтобы рассмотреть ряд интересных примеров, взятых
из химии и физики. Первый пример — это ион молекулы водорода. Положительно ионизированная молекула
водорода состоит из двух протонов и одного электрона, как-то бегающего вокруг них. Каких состояний
можно ожидать для этой системы, если расстояние между протонами велико? Ответ вполне ясен: электрон
расположится вплотную к одному протону и образует атом водорода в его наинизшем состоянии, а другой
протон останется одиночкой, положительным ионом. Значит, когда два протона удалены друг от друга, то
можно себе наглядно представить одно физическое состояние, в котором электрон «придан» одному из протонов.
Существует, естественно, и другое, симметричное первому состояние, в котором электрон находится возле
второго протона, а ионом оказывается первый протон. Эту пару состояний мы и сделаем базисными, обозначив
их |1> и |2>. Они показаны на фиг.
8.1. Конечно,
на самом деле у электрона возле протона имеется множество состояний, потому что их комбинация может
существовать в виде одного из возбужденных состояний атома водорода. Но нас сейчас не интересует это
разнообразие состояний, мы будем рассматривать лишь случай, когда атом водорода пребывает в наинизшем
состоянии — своем основном состоянии,— и пренебрежем на время спином электрона. Мы цросто предположим
*, что для всех наших состояний спин электрона направлен
вверх по оси
z.
Чтобы убрать электрон из атома водорода, требуется 13,5 эв энергии. Столько же энергии — очень
много по нашим теперешним масштабам — понадобится и на то, чтобы электрон оказался на полпути между
протонами (коль скоро сами протоны сильно удалены друг от друга). Так что по классическим понятиям
электрону немыслимо перескочить от одного протона к другому. Однако в квантовой механике это возможно,
хоть и не очень вероятно. Существует некая малая амплитуда того, что электрон уйдет от одного протона
к другому. Тогда в первом приближении каждое из наших базисных состояний |1> и |2> будет иметь
энергию En равную просто сумме энергий
атома водорода и протона. Матричные элементы H11 и H22
гамильтониана мы можем принять приближенно равными H0. Другие матричные
элементы H12 и H21, представляющие
собой амплитуды перехода электрона туда и обратно, мы опять запишем в виде —A.
Вы видите, что это та же игра, в какую мы играли в последних двух главах. Если пренебречь способностью
электрона перескакивать туда и обратно, то два состояния будут иметь в точности одинаковую энергию.
Эта энергия, однако, расщепляется на два энергетических уровня из-за того, что электрон может переходить
туда и назад, и чем больше вероятность перехода, тем больше расщепление. Стало быть, два уровня энергии
системы равны E0+A и E0-A,
и состояния, у которых такие энергии, даются уравнениями (8.7).
Из нашего решения мы видим, что если протон и водородный ион как-то расположить близко один
к другому, то электрон не останется подле одного протона, а будет перескакивать от протона к протону
и обратно. Если вначале он был близ одного из протонов, то затем он начнет колебаться туда и назад
между состояниями |1> и |2>, давая решение, меняющееся во времени. Чтобы получить решение, отвечающее
самой низкой энергии (которое не меняется со временем), необходимо, чтобы вначале система обладала
одинаковыми амплитудами пребывания электрона возле каждого из протонов. Кстати, вспомните, что электронов
отнюдь не два; мы совсем не утверждаем, что вокруг каждого протона имеется электрон. Имеется только
один электрон, и это он имеет одинаковую амплитуду (

по величине)
быть в том или ином положении.
Дальше, для электрона, который находится близ одного протона, амплитуда A
оказаться близ другого зависит от расстояния между протонами. Чем они ближе один к другому, тем больше
амплитуда. Вы помните, что в гл. 5 мы говорили об амплитуде «проникновения» электрона «сквозь барьер»,
на что по классическим канонам он не способен. Здесь то же самое положение дел. Амплитуда того, что
электрон переберется к другому протону, спадает с расстоянием примерно по экспоненте (для больших расстояний).
Раз вероятность, а следовательно, и значение A при сближении протонов возрастают,
то возрастает и расстояние между уровнями энергии. Если система находится в состоянии |I>, то энергия
E0 + A с уменьшением расстояния растет так,
что эти квантовомеханические эффекты приводят к силе отталкивания, стремящейся разнести протоны. Если
же система пребывает в состоянии |II>, то полная энергия при сближении протонов убывает; существует
сила притяжения, подтягивающая протоны один к другому. Эти энергии меняются с расстоянием между протонами
примерно так, как показано на фиг. 8.2. Тем самым у нас появляется квантовомеханическое объяснение
силы связи, скрепляющей ион H.
* До тех пор, пока нет сильных магнитных полей, это предположение впол¬не удовлетворительно. Влияние магнитных полей на электрон мы обсудим в цой же главе позже, а очень слабые спиновые эффекты в атоме водорода —
IIГЛ. 10.
Е
\ \ Е„ = Е0+А
^0^-~- Расстояние
^^"^ между
S^ протонами
Фиг. 8.2. Энергии двух стационарных состояний иона Нг" как функция расстояния между двумя протонами.
Однако мы позабыли об одной вещи. В дополнение к только что описанной силе имеется также электростатическая сила взаимного отталкивания двух протонов. Когда оба протона очень удалены друг от друга (как на фиг. 8.1), то «голый» про-тон видит перед собой только нейтральный атом, так что элек-тростатической силой можно пренебречь. При очень тесных сближениях, однако, «голый» протон оказывается порой «внут¬ри» электронного распределения, т. е. в среднем он ближе к протону, чем к электрону. Появляется некоторая добавочная электростатическая энергия, которая, конечно, положительна. Эта энергия — она тоже зависит от расстояния — должна (Выть включена в Е0, Значит, за Е0мы должны принять нечто похожее на штриховую кривую на фиг. 8.2; она быстро поды¬мается на расстояниях, меньших, чем радиус атома водорода. Энергию переворота А надо вычесть и прибавить к этому Е0. Если это сделать, то энергии Е, и ЕПбудут меняться с меж¬протонным расстоянием D, как показано на фиг. 8.3. [На ри¬сунке мы воспроизвели результаты более детальных выкладок.
179
Фиг. 8.3. Уровни энергии иона Н2как функция меж-протонного расстояния D{Ен=13,6 эв).
Межпротонное расстояние дано в ангстремах (1А=10~8см),. а избыток энергии над протоном плюс водородным ионом да-ется в единицах энергии связи атома водорода, так называе-мых «ридбергах» (13,6 эв).] Мы видим, что состояние |//) имеет точку минимума энергии — равновесную конфигу-рацию (условие наинизшей энергии) для иона Щ. Энергия в этой точке ниже, чем энергии отдельно протона и отдельно водородного иона, так что система связана. Отдельный элект¬рон действует так, что скрепляет протоны. Химик назвал бы это «одноэлектронной связью».
Этот род химической связи часто также называют «кванто-вомеханическим резонансом» (по сходству с двумя связанными маятниками, о котором мы уже говорили). Но звучит это таин¬ственнее, чем оно есть на самом деле; это только тогда «резо¬нанс», когда базисные состояния с самого начала неудачно выбраны, как у нас и было! А если выбрать состояние [//), вы сразу получите наинизшее энергетическое состояние и все.
Можно и по-иному объяснить, отчего энергия этого состоя¬ния должна быть ниже, чем у протона плюс атома водорода, Представим себе электрон возле двух протонов, удаленных па определенное, но не очень большое расстояние. Вы помните, что электрон возле одиночного протона «размазан» из-за прин« ципа неопределенности. Он ищет равновесия, пытаясь раздо¬быть "энергию пониже (низкую кулоновскую потенциальную энергию) и не оказаться при этом сжатым в пространстве че¬ресчур тесно, что привело бы к высокой кинетической энергии
(из-за соотношения неопределенности Ар&хягЩ. Если же про¬тонов два, то будет больше места, где у электрона может быть низкая потенциальная энергия. Он может размазаться (снижая тем самым свою кинетическую энергию), не повышая при этом своей потенциальной энергии. В итоге его энергия ниже, чем В атоме водорода. Тогда почему же у другого состояния |/>энергия выше? Но заметьте, что это состояние есть разность состояний |/> и \2).Вследствие симметрии |/> и \2)разность должна иметь нулевую амплитуду того, что электрон окажется на полпути между протонами. Это означает, что электрон не¬много сильнее ограничен в пространстве, что и приводит к большей энергии.
Следует сказать, что наше приближенное рассмотрение иона Щ как двухуровневой системы рассыпается впрах,- едва лишь протоны сблизятся до минимума энергии на кривой фиг. 8.3; тогда больше не получается хорошего значения истин¬ной энергии связи. На малых удалениях энергии двух «сос¬тояний» на самом деле уже не равны Е0; требуется более тонкое квантовомеханическое рассмотрение.
Положим, мы теперь заинтересуемся, что случилось бы, если бы вместо двух протонов у нас были два разных объекта, скажем один протон и один положительный ион лития (причем обе частицы по-прежнему имеют по единичному положитель¬ному заряду). В этом случае два члена Я^ и Я22 в гамильто¬ниане больше не совпадали бы; они были бы совершенно раз¬личны. Если бы оказалось, что разность (Я1Х—Я22) по абсо¬лютной величине много больше А——Ни, то сила притяжения €тала бы очень слабой. В этом можно убедиться следующим. образом.
Если в (8.3) подставить H^Hzi—A2, то мы получим
2 ± 2 У 1+(Я„-//„)»¦
(огда Ян—Я22 много больше Л2, корень довольно точно равец
1 , 2Л2
(я„-//22Г Гогда энергии обращаются в
Л2
?7 = Яи-
Л2 (8.8)
F—Н —
'Теперь они почти вплотную совпадают с энергиями Яи и Я25 Изолированных атомов и только чуть-чуть отличаются из-за наличия амплитуды перескока А.
180
181
Разность энергий (Е,—Еи) равна
(Яц-Я22) +77^17-.
Добавка к расстоянию между уровнями из-за переброса электрона уже не равна 2Л; она составляет А 1(Нг1—Я22) — часть этой величины (что по предположению много меньше единицы). Кроме того, сама зависимость Et—Епот расстояния между ядрами сейчас намного слабее, чем для иона HJ: в нее тоже входит множитель А/(Нц—Я22). Можно поэтому понять, от¬чего связь несимметричных двуатомных молекул, как правило,
очень слаба.
В нашей теории иона HJмы открыли объяснение механиз-ма, с помощью которого электрон, распределенный между двумя протонами, создает в итоге силу притяжения между ними даже тогда, когда они очень удалены друг от друга. Сила притяжения проистекает от уменьшения энергии системы, вы¬зываемого тем, что у электрона есть возможность прыгать от одного протона к другому. При таких прыжках система пере¬ходит от конфигурации атом водорода — протон к конфигура¬ции протон — атом водорода и обратно. Процесс символически можно записать так:
(Н,р)^(р,Н).
Сдвиг энергии, вызываемый этим процессом, пропорционален амплитуде А того, что электрон с энергией — №н (его энергия связи в атоме водорода) может от одного протона перейти к
другому.
При больших расстояниях Rмежду протонами электроста-тическая потенциальная энергия электрона близка к нулю почти во всем том пространстве, которое он вынужден преодо-леть, делая прыжок. Так что в этом пространстве электрон . движется почти как свободная частица в пустом пространстве, но обладая при этом отрицательной энергией! В гл. 1 [уравне-ние (1.7)] мы видели, что амплитуда для частицы определенной энергии перейти с одного места на другое, удаленное на рас¬стояние г, пропорциональна
e(«7ft) Pr
где р — импульс, отвечающий заданной энергии. В теперешнем случае (применяется нерелятивистская формула) р определя¬ется из выражения
.182
А это значит, что р — число мнимое:
р = IV2inWH
(другой знак перед корнем приводит к абсурду).
Стало быть, следует ожидать, что амплитуда А для иона И} будет меняться как
л-у?(»2рми . (8Л0)
при больших расстояниях Rмежду протонами. Сдвиг энергии,., вызываемый электронной связью, пропорционален А; значит, существует сила, сближающая два протона, которая пропор¬циональна (при больших R) производной от (8.10) по R.
Наконец, для полноты следует заметить, что, в одноэлектрон-ной системе с двумя протонами есть еще один эффект, кото¬рый тоже приводит к зависимости энергии от R. Мы 'пока им пренебрегали, поскольку он обычно не очень важен, за исклю¬чением как раз тех больших расстояний, на которых энергия обменного члена А убывает экспоненциально до очень малых величин. Новый эффект, о котором мы говорим,— это электро¬статическое притяжение протона к атому водорода, возникаю¬щее по той же причине, по какой любой заряженный предмет притягивает к себе незаряженный. «Голый» протон создает электрическое поле ?(изменяющееся как 1/R2) возле нейтраль¬ного атома водорода. Атом становится поляризованным, при¬обретая наведенный дипольный момент ц,, пропорциональный $. Энергия диполя есть и.
// представляется их линейной комбинацией:
представляется их линейной комбинацией: представляется их линейной комбинацией:
представляется их линейной комбинацией: (8.1)
(8.1) (8.2)
(8.2)

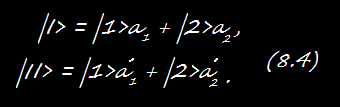
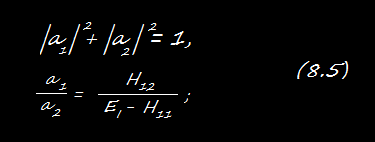

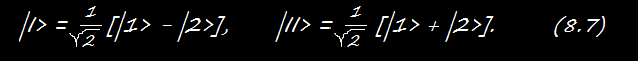
 по величине)
быть в том или ином положении.
по величине)
быть в том или ином положении.